Definition
- Configuration : 한 로봇의 모든 포인트들의 포지션을 정의할 수 있는 specification.
- C-space : 로봇의 모든 가능한 configuration을 포함하는 n-dimensional space.
- DOF(degrees of freedom) : robot의 configuration을 표현(정의)하는데 필요한 최소한의 dimension(좌표) 수.
- Rigid Body : 형태가 변경되지 않는 물체. 배게와 같이 힘을 주면 형태가 변화하는 물체는 rigid body가 아니다.
- Link : 로봇의 body. (rigid body만을 다룬다.)
- Joint : 로봇에서 links 사이를 연결하는 부품.
- Actuator : 로봇에서 motor와 같이 forces 또는 torques를 생성하여 link가 움직이도록 하는 부품.
Degrees of Freedom of a Rigid Body
3 차원에서 아래와 같은 rigid body가 있다고 가정하자.
- "A"는 (a, a', a'') 3개의 좌표로 표현 가능
- "B"는 (b, b', b'') 3개의 좌표로 표현 가능하지만 1개의 제약이 존재 (\( d_{AB} \)는 고정)
- "C"는 (c, c', c'') 3개의 좌표로 표현 가능하지만 2개의 제약이 존재 (\( d_{AC} \)/\( d_{BC} \) 사이의 거리는 고정)

rigid body 표면 위의 임의의 점들(A, B, C, D, etc.)의 freedom은 아래 표와 같이 정리된다.
| Point | coords | independent constraints | real freedom |
| A | 3 | 0 | 3 |
| B | 3 | 1 | 2 |
| C | 3 | 2 | 1 |
| D, etc. | 3 | 3 | 0 |
즉, 3차원 공간에서 rigid body는 6개의 freedom을 갖는다.
- point A를 나타내기 위해 3개의 좌표가 필요.
-> point A를 위해 x, y, z 좌표 3개를 결정하면 된다. - point B를 나타내기 위해 2개의 angle이 필요.
-> point B는 point A를 중심으로 하는 \( d_{AB} \)반지름을 갖는 구의 표면 위에 존재.
-> point B를 위해 구의 표면의 좌표를 결정하는 angles(latitude, longitude)을 결정하면 된다. - point C를 나타내기 위해 1개의 angle이 필요.
-> point C는 point A를 중심으로 하는 \( d_{AC} \)반지름을 갖는 구와
point B를 중심으로 하는 \( d_{BC} \)반지름을 갖는 구의 접점(원) 위에 존재.
-> point C를 위해 원의 외곽의 좌표를 결정하는 angle을 결정하면 된다.
이를 조금 더 일반적으로 표현하면 아래와 같다.
dof of rigid body = (sum of coords of the points) - (number of independent constraints).
- 3 dimension 공간에서 움직이는 rigid body는 spartial rigid body라고 하고 6개의 dof를 갖는다.
- 2 dimension 공간에서 움직이는 rigid body는 planar rigid body라고 하고 3개의 dof를 갖는다.
Degrees of Freedom of a Robot
앞에서 3차원 공간에서 rigid body는 6개의 dof를 갖고, 2차원 공간에서 rigid body는 3개의 dof를 갖는다는 것을 학습하였다. 우리는 앞으로 rigid body와 그들간에 연결(Joint)로 이뤄진 로봇에 대해서 다룰 것이다.
모든 Joint는 두개의 Link를 연결하고 (동시에 3개 이상의 link를 연결할 수는 없다.) Link의 움직임에 제약을 준다.
아래는 대표적인 Joint에 대한 설명이다.
| Joint | Image | Description | constraint for 2 planar rigid bodies |
constraint for 2 spartial rigid bodies |
| Revolute (R) |  |
hinge joint라고도 불리우며, joint axis에 대한 rotational 움직임을 허용한다. | 2 | 5 |
| Prismatic (P) |  |
sliding 또는 linear joint라고도 불리우며, joint axis 방향을 따라 translational(이동) 움직임을 허용한다. | 2 | 5 |
| Helical (H) |  |
screw joint라고도 불리우며, screw axis에 대한 rotational과 translational 움직임을 동시에 허용한다. | N/A | 5 |
| Cylindrical (C) | 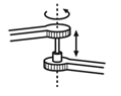 |
joint axis에 대한 rotational과 translational 움직임을 각각 허용한다. | N/A | 4 |
| Universal (U) |  |
두 개의 Revolute joint의 joint axis가 직각이 되도록 합친 것으로 각각의 rotational 움직임을 허용한다. | N/A | 4 |
| Spherical (S) |  |
ball and socket joint라고도 불리우며, 우리의 어깨와 같은 움직임을 허용한다. | N/A | 3 |
정리하면, rigid body와 joint로 이뤄진 로봇의 dof는 아래 식으로 표현할 수 있다.
dof of robot = Σ (body freedoms) – Σ (independent constraints from joints)
이를 Grubler's Formula 라고 한다. 식을 조금 더 정리하면 아래와 같다.
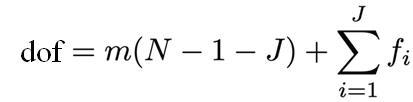
- m : spartial bodies는 6개, planar bodies는 3개
- N : rigid body의 수
- J : joint의 수
- \( f_{i} \) : joint의 constraint 수
'Robotics > Modern Robotics' 카테고리의 다른 글
| Modern Robotics - Configuration Space (2) - Topology/Representation/constraint (0) | 2022.04.01 |
|---|---|
| Modern Robotics - 강의 정보 (0) | 2022.02.01 |
